HW5: Gibberish Generator : Data Structures

Learn about probabilistic models of sequential data, like written or spoken language.
Get further practice with command-line arguments, files, etc.
Practice working with the Dictionary ADT.
Practice designing and creating a large software system.

Download the following ADT and implementation files (yes, even List; make sure your copy is up to date):

Also download the following five text files and store them alongside your code:

(I originally downloaded these files from Project Gutenberg, and then modified them slightly to make them easier to work with for this assignment.)

This is a partner assignment. Work with your assigned partner from class and submit only one copy of your work. As always, all partners' names should be in a comment at the top of the source code, and you should work by pair programming. No working remotely! You need to be sitting side by side.

Create a new Java file Gibberish.java with the class Gibberish in it, and a main method inside that.

A “Markov chain” is a mathematical model of a sequence of events: one event after another, unfolding through time. At any given point in time, the choice of event that happens next depends only on the event that is currently happening; there is no “memory” of previous events. For example, imagine a frog jumping among lily pads that has no memory of where it's been before. Its choice of the next lily pad it will jump to is influenced only by its current position: it can only jump to nearby pads, but it might very well jump right back to the one it just came from. The sequence of lily pads the frog visits could be modeled by a Markov chain. (Technically, this memorylessness only applies to “stationary Markov chains”; you can read more about Markov chains on Wikipedia.)

Here's a picture of a Markov chain:

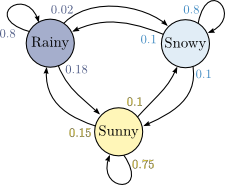
A Markov chain, which looks like a weighted directed graph with three nodes and nine edges — one edge from each node to each node, including self-loops. The nodes are labeled 'Rainy', 'Snowy', and 'Sunny', and the weights on the three edges out from each node sum up to 1. For example, Sunny has three outgoing edges: one to Snowy with weight 0.1, one to Rainy with weight 0.15, and one loop back to Sunny with weight 0.75.

This chain has three “states” — Rainy, Snowy, and Sunny — that correspond to events we might observe: a rainy day, a snowy day, or a sunny day. Between each pair of states is a transition: an arrow from one state to another (or to the same state), labeled with the probability of moving between those states. So, for example, this Markov chain says that if it's sunny on some particular day, there's a 75% chance it'll be sunny the next day too, a 15% chance it'll be rainy the next day instead, and a 10% chance it'll be snowy. Notice that the probabilities on the transitions out of each state all sum to 1 (or 100%).

Clearly a Markov chain isn't a perfect representation of the world; there's a lot more nuance to the weather than just fixed probabilities like in the picture above. But simplified mathematical models like these can still be useful (or, in our case, goofy and fun).

We can construct Markov chains by hand (for example, by looking at a picture of all the lily pads in the frog's pond), but we can also derive them directly from observations of sequences of states (for example, by counting how many snowy days follow sunny days in a whole year). This latter process is called “training” a Markov chain with a set of data.

In this assignment, you'll train a Markov chain on a body of text chosen by your user. The states will be words, and the transitions will correspond to probabilities of having a given word followed by some other word. You'll compute the transitions from the source text. Then you'll generate new sentences by hopping through the Markov chain (this is a technique called Markov chain Monte Carlo). The result each time is a nonsensical but reasonably well-structured sentence that carries some flavor of the source text.

From the picture above, it's clear that a Markov chain may be represented as a weighted digraph, where each edge weight is a transition probability, and the sum of weights out from each node is 1.0. As you'll see below, we use a different representation in order to simplify the training and sentence-generation tasks.

Create an interactive program that takes a filename as a command-line argument, trains a Markov chain on the text contained in the file, and then prints randomly-generated sentences from this chain until the user asks to quit.

An example run of the program would look like this:

> java Gibberish alice_test.txt
Press <Enter> to generate a random sentence; type "quit" to quit.  
  I think me the bank, and pictures or a mouse, you know.

Press <Enter> to generate a random sentence; type "quit" to quit.  
  Australia?

Press <Enter> to generate a random sentence; type "quit" to quit.  
  Dinah, tell me see: that she jumped up and picking the air!

Press <Enter> to generate a random sentence; type "quit" to quit.  exit
  [Sorry, I didn't understand that.]

Press <Enter> to generate a random sentence; type "quit" to quit.  quit
  [Okay, bye!]

Note the format of the prompts and responses; your program should have identically-formatted interactions with the user. If the user fails to specify a filename (valid or invalid) on the command line, print a helpful and well-formatted usage message, and then quit. If the specified file can't be read for any reason, print a descriptive error message and quit. Do not allow exceptions to bubble up to the user level.

Before you start programming, plan out the structure of your program, identifying small, distinct tasks and designing tools to solve each one. You have a lot of flexibility in how your structure your program; keep in mind that although I'm not telling you a specific way to do it, program design does count in the evaluation of your work. You may write everything in one class if you'd like, or divide it into multiple classes if you think that helps keep your program organized. Here are some design guidelines that will help you complete this assignment:

Plan out the structure of your program in advance, as best as you can. Think through how to break down the one big problem you have (write the program) into a bunch of separate subproblems (write just a function to get input from the user, for example). Then make empty functions for each of these subproblems.
Functions should be separated into those that interact with the user (receiving typed input or printing output to the screen), those that do sophisticated computations, and those that tie together the other pieces.
Provide a Javadoc comment for every function that you write, documenting its input, output, and behavior.
As you develop a sophisticated program, always try to keep it in a state where it runs (maybe incompletely) without producing errors. Add one feature at a time, always bringing your code back to a non-error-producing state before you try to add a new feature.
Mark each unimplemented feature with a “TODO” comment, and delete the comment once you've implemented the feature.

Detailed Description

Representing the Markov Chain

The states in your Markov chain will be words. Use a dictionary to represent the Markov chain, with each unique word as a separate key. The value associated with each key represents the full set of transitions away from that word. The value is a list of all the words that followed the key in the source text. For example, say our source text is:

Once upon a time there was a shadow upon the land, and in the field the sheep cowered in fright. One at a time they looked for the sun.

Here are all the key-value pairs for the dictionary representing the Markov chain trained on this text (lists are indicated by square brackets):

Key	Value
`"cowered"`	`["in"]`
`"they"`	`["looked"]`
`"sheep"`	`["cowered"]`
`"at"`	`["a"]`
`"the"`	`["land,", "field", "sheep", "sun."]`
`"field"`	`["the"]`
`"Once"`	`["upon"]`
`"a"`	`["time", "shadow", "time"]`
`"upon"`	`["a", "the"]`
`"fright."`	`["One"]`
`"in"`	`["the", "fright."]`
`"shadow"`	`["upon"]`
`"One"`	`["at"]`
`"time"`	`["there", "they"]`
`"looked"`	`["for"]`
`"for"`	`["the"]`
`"land,"`	`["and"]`
`"was"`	`["a"]`
`"there"`	`["was"]`
`"and"`	`["in"]`

Notice that this dictionary has one key for each unique word in the sentence (except the last word, since it has no successors).

Notice also that we don't explicitly represent transition probabilities here. Instead, to transition out of a state, we will just pick a random entry from the list of possible next states; states may be repeated in this list (like “time” in the list for “a”) and thereby be more likely to be chosen.

Notice also that the value associated with each key is always a list, even if that list contains only one item.

Training the Markov Chain

The states in your Markov chain will be all the “words” in the file. A “word”, for our purposes, is just a sequence of non-whitespace characters, separated from other words by one or more whitespace characters. (Whitespace characters are spaces, newlines, tabs, etc.) You may have to do some additional work to make sure that your list of words doesn't contain any empty strings; sometimes those can crop up.

(Notice that in the example dictionary above, capitalization and punctuation were included in words. So "The" and "one" would be considered different words, as would be "sun." and "sun" and "Sun". This is intentional; it adds to the quality of the sentences you generate. So make sure that you don't remove capitalization or strip punctuation!)

So, once you've got this list of words, step through it one-by-one and build the transition lists. Be careful about your running time! If we assume that dictionary operations and appending to the end of a list are all O(1) operations, than the running time of your training function should be linear in the number of words. (This means that you should do only constant work per word.)

Choosing Starting Places

Before we can start bouncing around the Markov chain, we need to know where to start. This start state will be the first word of our sentence. Naturally, we need to choose one of the states whose word is capitalized. To make this choice easy, you will first generate a list of all the keys that begin with a capital letter. We'll call these “start words”. (Note that generating the list of start words from the dictionary keys means that each start word will have equal probability of being chosen, even if one shows up much more often in the sample text than another. This is intentional; it makes our gibberish sentences weirder.)

Generating Sentences

To generate a sentence from the Markov chain, we first pick a random start word, then pick the next word by choosing randomly from the list associated with that start word in the dictionary. Then we pick the next word after that by choosing from the list associated with the current word. We keep doing this until we reach an “end word” — one whose last character is ., ?, or !. At this point, we can construct a single string by joining together, in order, all the states that we visited. (You may wish to use the Java StringBuilder class.)

Note that the example text files I gave you have all the quotation marks, parentheses, etc. stripped from them, so that this simple rule for identifying end words will work. If you'd like to use other text samples (which you should! It's fun!), you'll either need to manually or automatically strip out the quotation marks, etc., or build a more sophisticated function for testing whether a given word is an end word.

Suggestions

Here's how I would break up the problem, if I were to write the solution all in one class using static functions only:

main() — Runs the whole show.
parseFile() — Given a filename, returns a Scanner that will return one word at a time from the file.
trainMarkovChain() — Given a Scanner, trains the Markov chain and returns the corresponding dictionary.
getStartWords() — Identifies all the start words among the keys of a given dictionary (and returns them as a list).
isEndWord() — Returns true or false, depending on whether a word ends with sentence-ending punctuation.
randomSentenceLoop() — Repeatedly asks the user whether to generate a new random sentence or quit, and prints out the sentence if requested.
makeRandomSentence() — Returns a string produced by a random walk through a given Markov chain.

Submit your program on Canvas.

Interactivity — 1 points
Correctness of Markov-chain training — 8 points
Efficiency of Markov-chain training — 2 points
Random sentence generation — 7 points
Program organization — 3 points
Comments and style — 4 points

HW5: Gibberish Generator

Goals

Setup and Requirements

Background