Re-read sections 2.2 and 2.4 in the book, paying particular attention to summation, double-summation, and matrix multiplication.
As a supplement to section 2.4, here's an example of matrix multiplication that I find helpful to think about.
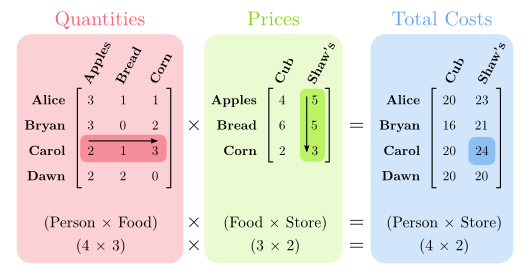
Say we have four people (Alice, Bryan, Carol, and Dawn), each of whom has a shopping list (a certain number of each of three items — Apples, Bread, and Corn — that they'd like to buy). And say each person is considering two different grocery stores, Cub and Shaw's, each of which has a different price for each different food item. We want to find out the total cost of each person's shopping list at each store.
To find out the cost of Carol's shopping list at Shaw's, for example, we need to multiply the number of apples Carol wants by the price of apples at Shaw's ($2 \cdot 5$), plus the number of loaves of bread times the price for bread ($1 \cdot 5$), plus the number of ears of corn times the price for corn ($3 \cdot 3$). The total cost, 24, is what Carol would pay for her whole shopping list at Shaw's. (If you're familiar with vector arithmetic, you might recognize this as the dot product of Carol's shopping list with the price list at Shaw's.)
What matrix multiplication does is compute all of these sums-of-products in one go. We arrange the shopping lists as the rows of the left matrix, and the price lists as the columns of the second, and then multiply the matrices together:

Remember that we always write the size of a matrix as “rows-by-columns”. So the shopping-list matrix is 4×3, and the store-price matrix is 3×2.
This explains why the “inner sizes” in a matrix multiplication — the number of columns in the left matrix and the number of rows in the right one — must match: because the column labels on the left are for food items, as are the row labels on the right. Another way to look at it is that every shopping list needs a quantity for each food item, and each store's price list needs a price for each food item.
It also explains why the “outer sizes” carry over to the result of multiplication: we have one shopping list per person, and one set of prices per store, so in the end we're left with a set of values that correspond to each (person, store) pair. We've “summarized over” that inner Food dimension.
Before you move on with the questions, look carefully at the formula that defines matrix multiplication, which is Definition 2.43 in your book. Say we have two matrices $A$ and $B$. $A$ is $n \times m$, and $B$ is $m \times p$. If we multiply them together — $AB = M$ — we get an $n \times p$ matrix $M$ whose entry in row $i$, column $j$ is:
$$ M_{i,j} = \sum_{k=1}^{m}A_{i,k}B_{k,j}. $$All this says is that we move across row $i$ in matrix $A$, and down column $j$ in matrix $B$, multiplying corresponding values together as we go, and adding all of these products up. Study the formula and try to see the connection.
One last thing: remember that there is nothing in any way special about the choices of the variable names $i$, $j$, and $k$ in the formula above. $k$ is just the “loop variable” for the summation, and $i$ and $j$ name the position in matrix $M$ that we're trying to compute a value for. You should be prepared to substitute these variable names for others when you start working with compound matrix multiplications and so forth.
Do these problems from the book, listed on page 221.
Here's one simple property of summation. If we have a scalar value (just a regular real number) $k$, and we're summing values over some index $i$, then:
$$k \sum_i x_i = \sum_i k x_i$$That is, if you are multiplying a summation by a multiplicative factor that is constant with respect to the change of that summation's index (as $k$ is above), that factor can go inside or outside the summation. There's nothing mysterious about this; the above statement is just a more compact and formal way of writing the following:
$$k (x_1 + x_2 + \ldots x_n) = kx_1 + kx_2 + \ldots kx_n$$This is obviously true, due to the distributive property of scalar multiplication over scalar addition.
Here is a slightly more complicated theorem:
$$ \begin{align*} \sum_i \Big( x_i \sum_j y_j \Big) &= \sum_i \Big( \sum_j x_i y_j \Big)\\ &= \sum_j \Big( \sum_i x_i y_j \Big) = \sum_j \Big( y_j \sum_i x_i \Big) \end{align*} $$That is, if you have nested summations of products of things that are entirely independent of each other's summation index, then you can switch the order of the summation at will.
Write an argument for the correctness of each of the three equalities in this theorem. You don't have to write proofs, per se, but your arguments should be rigorous and convincing, without making any assumptions other than that $x$ and $y$ are finite sequences of real numbers, not necessarily of the same length. For example, my argument for each equality is just a carefully-written expansion of the summation notation, like the distributive-property equation above, accompanied by a couple sentences. (Hint: Start by working out an example where $x$ is a sequence of three distinct numbers, and $y$ is a sequence of four other distinct numbers. Work out all the terms in each summation, and think about how to arrange them on the page so that their patterns become clear.)
Then do these problems, listed on page 251–252.