Fibbly.
By Jadrian Miles. 1993–2010.Fibbly is an interactive visualization of a particular type of number sequences that I've been playing around with throughout my life. It is designed to serve both as a tool for mathematical investigation and as a work of visual art.
If you'd rather look and play than read about the piece, please see the still image gallery or a video, or just interact with Fibbly yourself.
Third Grade.
One day in third grade, I had an idea: start with 0 and 1, add them together to get 1, and then repeat: add 1 and 1 together to get 2, add 1 and 2 to get 3, add 2 and 3 to get 5...
This pattern leads to ever-larger numbers, but I wanted to keep the numbers small. So I came up with an additional rule: if the sum of the numbers has more than one digit, just use the last digit and ignore the rest. Thus the next terms are:
- 3 + 5 = 8
- 5 + 8 = 13 (written as 3)
- 8 + 3 = 11 (written as 1)
- 3 + 1 = 4...
I soon wrote down the following sequence of 60 digits:
0 1 1 2 3 5 8 3 1 4 ... 5 9 4 3 7 0 7 7 4 1 ... 5 6 1 7 8 5 3 8 1 9 ... 0 9 9 8 7 5 2 7 9 6 ... 5 1 6 7 3 0 3 3 6 9 ... 5 4 9 3 2 5 7 2 9 1
At the end, you can see that the sequence loops back on itself and repeats from the beginning:
- 9 + 1 = 10 (written as 0)
- 1 + 0 = 1
- 0 + 1 = 1
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5...
Fifth Grade.
A couple years later, I learned that the sequence of numbers generated by this process, ignoring the digit-dropping rule, is quite well-known: it's the Fibonacci sequence, which has been studied for centuries and appears in many natural phenomena.
0 1 1 2 3 5 8 13 21 34 55 89 144 ...
The sequence I'd written down, then, was the last digit of each of the Fibonacci numbers, and I had learned an interesting property of them:
The last digit of the Fibonacci numbers repeats after 60 terms.
Seventh Grade.
In seventh grade, I realized that the choice of 0 and 1 as the starting numbers for the sequence was somewhat arbitrary. Why not start with 1 and 2?
1 2 3 5 8 3 1 4 5 9 ... 4 3 7 0 7 7 4 1 5 6 ... 1 7 8 5 3 8 1 9 0 9 ... 9 8 7 5 2 7 9 6 5 1 ... 6 7 3 0 3 3 6 9 5 4 ... 9 3 2 5 7 2 9 1 0 1
Or how about 3 and 8?
3 8 1 9 0 9 9 8 7 5 ... 2 7 9 6 5 1 6 7 3 0 ... 3 3 6 9 5 4 9 3 2 5 ... 7 2 9 1 0 1 1 2 3 5 ... 8 3 1 4 5 9 4 3 7 0 ... 7 7 4 1 5 6 1 7 8 5
These sequences are the same as the first one, just shifted around to start at different terms. I call the pair of starting numbers used to generate a sequence the "seed" for that sequence. Since the sequence above repeats itself after the end, any consecutive pair of numbers in it, used as a seed, will generate the same sequence. There are 60 numbers in the sequence, and thus 60 seeds that generate it.
There are 100 possible pairs of digits 0–9, though. Which seeds aren't accounted for? What sequences do they generate? I wrote them all down and came up with this list:
0 2 2 4 6 0 6 6 2 8 0 8 8 6 4 0 4 4 8 2
0 5 5
1 3 4 7 1 8 9 7 6 3 9 2
2 6 8 4
Note that all these sequences, just like the 60-term one above, repeat at the end. These sequences have, respectively, 20, 3, 12, and 4 terms. 60 + 20 + 3 + 12 + 4 = 99, and the missing pair is (0, 0), which generates a trivial sequence of just
0
Ninth Grade.
In reading about the Fibonacci numbers, I learned of the Fibonacci spiral, which is created by connecting quarter-circle arcs with lengths proportional to subsequent terms in the Fibonacci sequence.
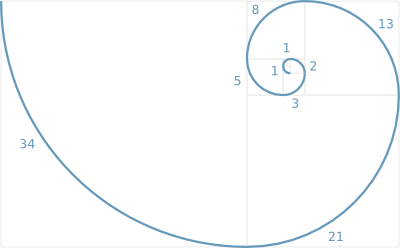
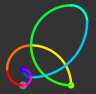
I used the same abstract drawing rule (a quarter-circle up and left, the next up and right, the next down and right, the next down and left, then the next up and left, and so on, each arc proportional in length to its corresponding term of the sequence) to create a curvy figure for the 60-term sequence above. A zero term is interpreted in this system by staying in the same place but moving on to the next arc orientation, essentially drawing a zero-length arc.
A surprising result is that the curve, like the sequence, repeats after 60 terms: it ends at the starting position and in the same orientation, so that if you continued drawing it, you would trace back over the original lines.
Here's how this figure appears in Fibbly, which color-codes the curve segments in order around the color wheel (that is, the arc for the first term is red, arcs for later terms are colored orange, terms later still are yellow, and so on):
The other sequences generate curves with other interesting properties.

0 2 2 4 6 ... also loops
back on itself.
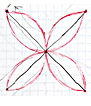

0 5 5 takes four repetitions
for the curve to repeat.
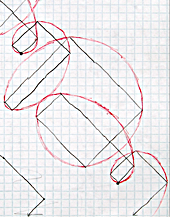

1 3 4 7 1 ... ends in a
different place than it begins, but in the same orientation, so continuing to
draw the curve moves ever further from the starting point. I call this type
of curve "periodic".

2 6 8 4 is also periodic.
I guess I forgot to draw this one.
Tenth Grade.
In tenth grade I realized another generalization of the rule for generating these sequences: why choose only two numbers for a seed? Why not three? I started with (0, 0, 1), added them together to get 1, added 0, 1, and 1 to get 2, and kept writing:
0 0 1 1 2 4 7 3 4 4 1 9 4 4 7 ... 5 6 8 9 3 0 2 5 7 4 6 7 7 0 4 ... 1 5 0 6 1 7 4 2 3 9 4 6 9 9 4 ... 2 5 1 8 4 3 5 2 0 7 9 6 2 7 5 ... 4 6 5 5 6 6 7 9 2 8 9 9 6 4 9 ... 9 2 0 1 3 4 8 5 7 0 2 9 1 2 2 ... 5 9 6 0 5 1 6 2 9 7 8 4 9 1 4 ... 4 9 7 0 6 3 9 8 0 7 5 2 4 1 7 ... 2 0 9 1
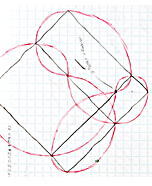
This sequence has 124 terms. It makes sense that there would be many more terms in this sequence than the others, since there are 1000 possible three-element seeds made of the numbers 0–9. I drew the curve for it, but it was a total mess, and that drawing has been lost to the mists of time. The curve is huge and periodic; you can see it to the left.
For reasons that will be explained below, Fibbly only covers sequences with two-element seeds. You can generate sequences from three-element seeds using the Fibbly curve tool.
Eleventh Grade.
In my junior year of high school, I took Number Theory and learned about modular arithmetic. In modular arithmetic, numbers "wrap around" a particular chosen number M, the so-called modulus. Counting up from zero with the modulus M = 6 gives the following repeating sequence:
0 1 2 3 4 5 0 1 2 3 4 5 0 1 2 3 ...
1 and 7 are said to be congruent modulo 6, because counting to 7 with this modulus wraps you around to 1. Equivalently, the remainder of dividing 7 / 6 is 1. In number theory, this fact is written with the following notation:
7 ≡ 1 (mod 6)
The above statement is read as "seven is congruent to one mod six". Computer programmers write the same thing more concisely using the modulo operator, %:
7 % 6 = 1
This reads as "seven mod six equals one".
It's easy to see that dropping all but the last digit of a number is the same as evaluating it mod 10, so my original 60-term sequence is just the Fibonacci sequence mod 10. This suggests yet another generalization: why only use 10 as the modulus? Why not wrap sums around 8?
Or 18? The sliders marked "mod" in Fibbly and the Fibbly curve tool control the modulus of the sequences. Mess around with them and see what curves you can make!College.
During my college years I learned more about computer programming and eventually wrote a program in PHP to compute Fibbly sequences and draw their curves on the screen with SVG. It was a little clunky, but the computer freed me from having to do calculations and drawings by hand, and I started wondering about higher-level patterns in the behavior of these sequences. I computed statistics about sequence lengths and the distribution of zeros in the sequences, but ultimately didn't get very far with it.
My senior year of college, I took a class in electronic music composition, and turned to the Fibbly rule to generate melodic and percussive motifs. The result was a little rough, since it was the first piece of music I ever composed, but I like it pretty well.
Grad School.
In grad school, I volunteered at New Urban Arts, an art mentoring program for high school students in Providence, RI. Rather than helping kids with art, I tutored them in math and other subjects. As a side benefit, I also got to participate in the staff art exhibition, so I decided to rewrite the curve-drawing program to be pretty and interactive and install it for the show. The Fibbly curve tool, projected on the wall in the front shop window and accompanied by my electronic composition from college, was the result.
While preparing for the show, I talked to a lot of students and colleagues at New Urban Arts about the Fibbly sequences and how they'd been weaving in and out of my life for years. I explained as much of the math as people were willing to listen to, and in doing so gave myself an idea for further exploration.

We established above that picking any consecutive pair of numbers out of a Fibbly sequence and using them as the seed for a new sequence (keeping the modulus fixed) will actually result in the same sequence, just shifted around to start at a different position. But given two sequences, how can we determine whether they're the same?
The easiest way is to establish a consistent system for assigning a unique name or label to a sequence that doesn't change if you shift its terms. If two sequences have the same label, they must be the same sequence, just shifted around. The label I came up with is what I call the "standard seed": the lowest consecutive pair of numbers (in dictionary order) that appears in the sequence. The standard seed for
1 8 9 7 6 3 9 2 1 3 4 7
is (1, 3), and the standard seed for
3 4 7 1 8 9 7 6 3 9 2 1
is also (1, 3)—keep in mind that we have to consider the pair of numbers that wraps around to the beginning of the sequence. Since these two sequences have the same standard seed, we determine that they are actually the same sequence, just shifted.
We may extend this "standard seed" concept to talk about seeds rather than sequences. The standard seed of a given seed, say (1, 8), is the standard seed of the sequence that that seed generates—in this case, (1, 3).

For seeds of length 2, the entire set of seeds for a given modulus may be represented by a grid: numbering the rows and columns from 0 to M-1, the grid point at row i and column j represents the seed (i, j). The figure below shows all the seeds for M = 4.
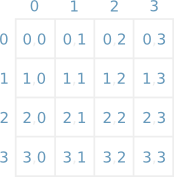
On Thanksgiving night, 2009, I stayed up late at my parents' house writing down the standard seeds for all the seeds for a handful of moduli, arranging them on grids.

Standard seeds for mod 8. Click for others.
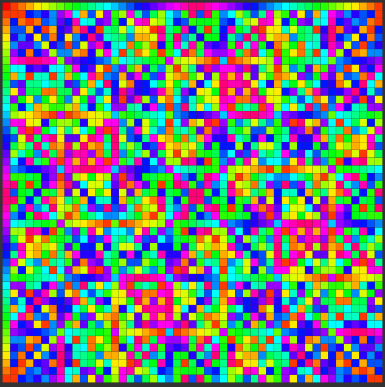
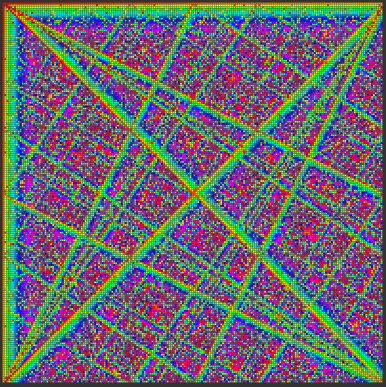
By labeling seeds by their standard seeds, we establish a so-called equivalence relation among seeds for a given modulus. Two seeds are considered equivalent if their standard seeds are the same; they are not equivalent if their standard seeds differ. Equivalent seeds are said to belong to the same equivalence class. The "fractal" visualization on the left side of Fibbly assigns a unique color to each equivalence class and colors a grid according to the equivalence class of the seed at each grid point.

Equivalence classes for mod 8.

Equivalence classes for mod 10.
For mod 10, we see that there are six colors, and thus six equivalence classes, corresponding to the six different sequences I wrote down in seventh grade. The higher the modulus, the more grid points, and the more detail in the pattern of equivalence classes. As you explore higher moduli, you'll notice recurring themes in the visual arrangement of the equivalence classes. These patterns are inherent properties of the equivalence classes; they were not designed by a person. Art (and math) of this sort is more akin to landscape photography than to painting: the artist simply observes and discovers, rather than creating.
We could extend the same seed-grid scheme to seeds with three terms each by constructing a three-dimensional grid, a cube. This is difficult to represent on a computer's 2-D display, hence the restriction of Fibbly to only seeds of length 2.

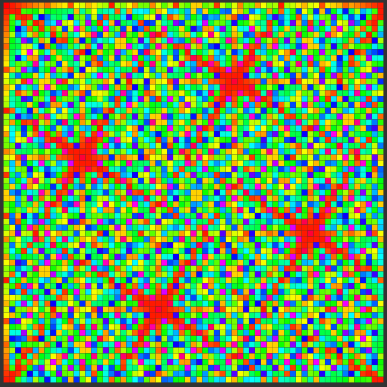
Fibbly connects the equivalence class grid view to the single-sequence curve view through interaction: if you click on any colored square in the equivalence class grid, the curve for the resulting sequence gets drawn in the background. The other seeds in the equivalence class turn black, too, so you can see the pattern they form. Mod 17, for example, exhibits striking symmetry:
Depending on how fast your computer and web browser are, you can move your seed selection around rapidly and watch how the pattern of equivalent seeds changes. Mod 67 and mod 76 are two of my favorites for this.

As I mentioned in the introduction, Fibbly is both a tool for mathematical investigation and a work of visual art. I hope to eventually write some proofs about patterns I've noticed in the visualizations, but even without proofs I think the visualizations are beautiful and fun to play with. Please get in touch if you like this work or discover something you think is interesting!