The Problem
This is the task of computing the set of all the vertices in the connected component of a given vertex. For example, in the following graph, the connected component that includes vertex 5 is the vertex set $\{5, 8, 3, 2, 4\}$:
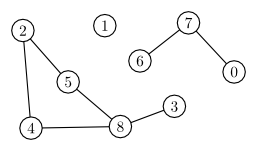
The Algorithm
Given a graph $G = (V, E)$ and a vertex $s$ in that graph, an algorithm to compute the connected component of $s$ may be built on top of breadth-first search. Here's how it works:
- Let $n = |V|$. ($|V|$ is the number of vertices in the graph.)
- Create an empty queue called $Q$.
- Create a list, $D$, of length $n$. (This list will store the number of edges it takes to get from $s$ to each other vertex $i$.)
- Set $D[i] = -1$ for all $i = 0, 1, 2 \ldots (n-1)$. (At the beginning of the algorithm, we don't know how many steps it takes to get from $s$ to any other node, so we use the sentinel value -1 to indicate that.)
- Set $D[s] = 0$ and enqueue $s$ in $Q$.
- While $Q$ is not empty:
- Dequeue a vertex from $Q$ and call it $v$.
- For each neighbor $u$ of $v$:
- If $D[u] = -1$, set $D[u] = D[v] + 1$ and enqueue $u$ in $Q$.
- We have now computed the connected component of $s$: each vertex $i$ for which $D[i] \ge 0$ is in $s$'s connected component.
Take a few minutes to think through why this algorithm works. What makes this a breadth-first search? (The answer is more fundamental than “it uses a queue”.) How do we know that all the vertices in $s$'s connected component have been given a non-negative value in $D$ by the time the while loop exits? How do we know that this algorithm will terminate (that is, that it won't run forever)?
Your Implementation Instructions
Implement the above algorithm in a method with the following signature:
/** * Computes and returns the list of all vertices in the graph G that are in the * same connected component as a specified node. * * @param G The graph in which to search. * @param targetNode The ID of a node in G. * * @return A List of node IDs (with no repeats) of the nodes in G that are in * targetNode's connected component. */ public static List<Integer> connectedComponent(Graph G, int targetNode)
Note that the algorithm was described in prose using mathematical notation, so the variable names are very short, as is standard in math. When you implement it in code, you should use descriptive variable names.
An Extra Challenge
This step is optional; it's just here for fun if you want to try implementing an extra feature.
Create another method that computes all of a graph's connected components:
/** * Computes and returns all the connected components of a graph. * * @param G The graph in which to search. * * @return A List of Lists of node IDs. Each inner list represents a single * connected component of G: its contents are the IDs (with no repeats) of all * the nodes in the component. The full output accounts for every node in G, * and lists each node only once. */ public static List<List<Integer>> allConnectedComponents(Graph G)
The algorithm to do this involves just a small modification to the single-component algorithm given above.
Problem 2: Detecting a Cycle
The Problem
This is the task of computing a set of vertices that form a cycle somewhere in the connected component of a given vertex. For example, in the following graph, the cycle $(2, 4, 8, 5)$ is in the connected component that includes vertex 3:

The Algorithm
Given a graph $G = (V,E)$ and a vertex $s$ in that graph, an algorithm to detect a cycle in $s$'s connected component (if there is one) may be built on top of depth-first search. Here's how it works:
First, set everything up to do the search:
- Let $n = |V|$.
- Create an empty stack called $S$.
- Create a list, $P$, of length $n$. (For each vertex $i$, $P[i]$ will store $i$'s “predecessor” — the vertex we came from to get to $i$.)
- Set $P[i] = -1$ for all $i = 0, 1, 2 \ldots (n-1)$. (We haven't visited anything yet.)
- Set $P[s] = s$ and push $s$ onto $S$.
- Let $c = -1$. ($c$ will be the ID of a single node in a cycle, if we find one.)
Then search the graph for a cycle:
- While $S$ is not empty and $c = -1$:
- Pop a vertex from the top of $S$ and call it $v$.
- For each neighbor $u$ of $v$:
- If $P[u] = -1$:
- Set $P[u] = v$.
- Push $u$ onto $S$.
- Otherwise, if $u \ne P[v]$:
- Set $c = u$. (We've detected a cycle!)
- Set $P[P[u]] = u$.
- Set $P[u] = v$.
- Immediately break out of the for loop.
- If $P[u] = -1$:
Finally, reconstruct the cycle from the values you computed.
- If $c = -1$, then there are no cycles in $s$'s connected component, and we're done.
- Otherwise, the values in $P$ tell us how to walk backward around the cycle from $c$. So:
- Create an empty list, $C$.
- Add $c$ to the end of the list, and let $v = P[c]$.
- While $v \ne c$:
- Add $v$ to the end of the list.
- Let $v = P[v]$.
- Return $C$.
Take a few minutes to think through why this algorithm works. What makes it a depth-first search? How can we be certain we'll find a cycle if there is one to be found in $s$'s connected component? How do we know, when we perform the “Otherwise, ...” step, that the vertex $c$ is a member of a cycle? Why do we have to check the condition $u \ne P[v]$ before we decide that? (What would happen if we didn't check?)
Your Implementation Instructions
Implement the above algorithm in a method with the following signature:
/** * Computes and returns a list of vertices in some cycle in the connected * component of a specified vertex in a graph. * * @param G The graph in which to search. * @param targetNode The ID of a node in G. * * @return An empty list if there are no cycles in targetNode's connected * component. Otherwise, a list of node IDs (with no repeats), in order, around * some cycle. There is an edge between the first and last nodes in this list. */ public static List<Integer> findCycle(Graph G, int targetNode)
Submission and Grading
Submit your GraphTraversal.java file on Moodle.
Start early, ask lots of questions, and have fun!
Assignment requirements
This is a partial list of the things that we'll be looking for when evaluating your work:
- The class has no non-static methods or members in it.
- The methods
connectedComponent()andfindCycle()are implemented and correct. - The main method tests all public methods with some interesting and challenging inputs. (Remember that “big” is not the only type of “challenging”; if your algorithm is correct on small graphs it will be correct on big ones too, but not vice-versa.)
- The algorithms use only the ADT interfaces and implementations provided.
Grading
- Assignment Requirements — 20 points
- Comments, Style, and Design — 5 points